Durante los últimos diez años, la astrofísica ha entrado en una lujosa era de disponibilidad pública de datos. Prácticamente todas las misiones espaciales y telescopios terrestres modernos incluyen en sus presupuestos costosos centros de distribución de datos, garantizando así, el acceso de toda la comunidad científica a los mismos. Dado que es prácticamente imposible diseñar un instrumento o telescopio que pueda operar de forma óptima en rangos muy amplios de longitud de onda, normalmente cada instrumento está optimizado para trabajar en una región relativamente estrecha del espectro. En consecuencia, para obtener una cobertura abundante de líneas espectrales, muchos estudios han combinado datos procedentes de diferentes telescopios o misiones.

En muchos casos, los objetos a estudiar evolucionan en escalas temporales muy grandes (por ejemplo, observaciones de galaxias o del medio interestelar) y, por lo tanto, estas observaciones no tienen que ser estrictamente simultáneas. Sin embargo, cuando se trata de eventos u objetos transitorios, las observaciones deben ser tomadas de forma simultánea por todos los telescopios (por ejemplo, observaciones de explosiones supernova o del Sol) y esto es mucho más complicado de obtener. Sin embargo, el esfuerzo de coordinar varios observatorios para obtener información en diferentes partes del espectro merece la pena. Por ejemplo, en el caso de observaciones solares, solamente hay unas pocas líneas en el visible que son sensibles a la cromosfera. Pero si nos vamos al ultravioleta, encontramos líneas como Mg II h&k que además nos dan información de la alta cromosfera y de la región de transición con la corona.

Uno de los principales problemas que se pueden encontrar al intentar interpretar este tipo de conjuntos de datos es la discrepancia de la resolución espacial entre las diferentes regiones espectrales, dado que cada instrumento / telescopio nos proporcionará una resolución diferente. Para hacer estudios cualitativos, podemos simplemente hacer un mapeado de los datos de baja resolución a la malla de más alta resolución. Pero en el momento en que queramos hacer un modelado conjunto de los datos, vamos a ver una discrepancia entre la predicción del modelo y los datos, dado que los píxeles de los datos de más baja resolución representan un promediado espacial más extenso en la superficie del objeto. La Ilustración 1 muestra un ejemplo de co-observación en el visible con el Telescopio Solar Sueco (SST, Scharmer et al. 2003) y el ultravioleta con el satélite de la NASA IRIS (de Pontieu et al. 2014). La discrepancia de resolución es de aproximadamente un factor 4.42.

Una discrepancia de resolución en las diferentes ventanas espectrales de los datos, suele conllevar que el modelo reconstruido sólo alcanza la resolución de la ventana espectral con peor resolución espacial y, además, pueden aparecer artefactos, ya que el código podría no ajustar bien las diferentes ventanas espectrales (Vissers, G. J. M. et al. 2019). La Ilustración 2 muestra un ejemplo de este efecto. En ella, hemos preparado una simulación de los datos que se obtendrían de una co-observación típica utilizando SST y IRIS. En cada punto de esa imagen tenemos un espectro espacialmente resuelto de Ca II K, Mg II k, Ca II 854.2 nm y Fe I 617.3 nm. Tras aplicar una inversión NLTE tradicional a estos datos sintéticos, obtenemos, entre otros, la temperatura, de la que mostramos un corte horizontal en la cromosfera en el panel central de la Ilustración. En ella, se aprecia como la presencia de los datos de IRIS, que simplemente han sido re-interpolados a la malla de SST, emborrona la reconstrucción de la temperatura en la cromosfera si no se tiene en cuenta el efecto de la discrepancia de resolución.

Para tener en cuenta esta discrepancia, hemos desarrollado un método, basado en el algoritmo de Levenberg-Marquardt para ajustes no-lineales, que incluye en el modelo todos los procesos de muestreado, degradación y rotación que sufre el haz de luz desde que entra en el telescopio hasta que llega al detector (de la Cruz Rodríguez, J. 2019). La idea se basa en la inclusión de un operador lineal de degradación espacial en la definición de la función de mérito a minimizar:

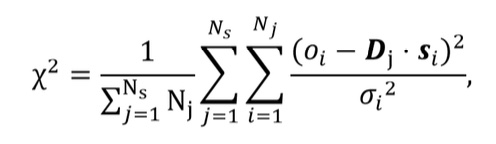
donde, Ns es el número de ventanas espectrales, N_j es el número de mediciones dentro de una ventana espectral, D_j es el operador total de degradación, que actúa sobre los datos sintéticos s_i en todo el campo de visión para esa longitud de onda y σ_i es la estimación del nivel de ruido. El acoplamiento espacial se introduce en el producto D_j·s_i, dado que el espectro sintético se genera a partir de los parámetros físicos del modelo que estamos reconstruyendo.

Estos operadores lineales son matrices en las que cada fila representa un punto degradado en la salida y cada columna representa cómo este punto está afectado por los parámetros del resto del campo de visión. La Ilustración 3 muestra varios ejemplos de estos operadores y cómo pueden combinarse con un simple producto matricial. El principal efecto de introducir operadores que acoplan la solución de diferentes puntos es que la inversión se convierte en un problema global, y las correcciones deben calcularse de forma simultánea para todo el campo.

Bajo esta aproximación, el sistema lineal que debemos resolver en cada iteración tiene dimensiones (n_x×n_y×n_p)², aunque la matriz puede ser relativamente dispersa. De esta forma, un campo de visión con 256 puntos en cada dirección y 5 parámetros libres implica resolver un sistema de ecuaciones con 327680² elementos (800 GB en doble precisión si todos los elementos son no-ceros que debemos almacenar en la RAM), que debe resolverse de forma iterativa (usando métodos como GMRES o BiCGStab).

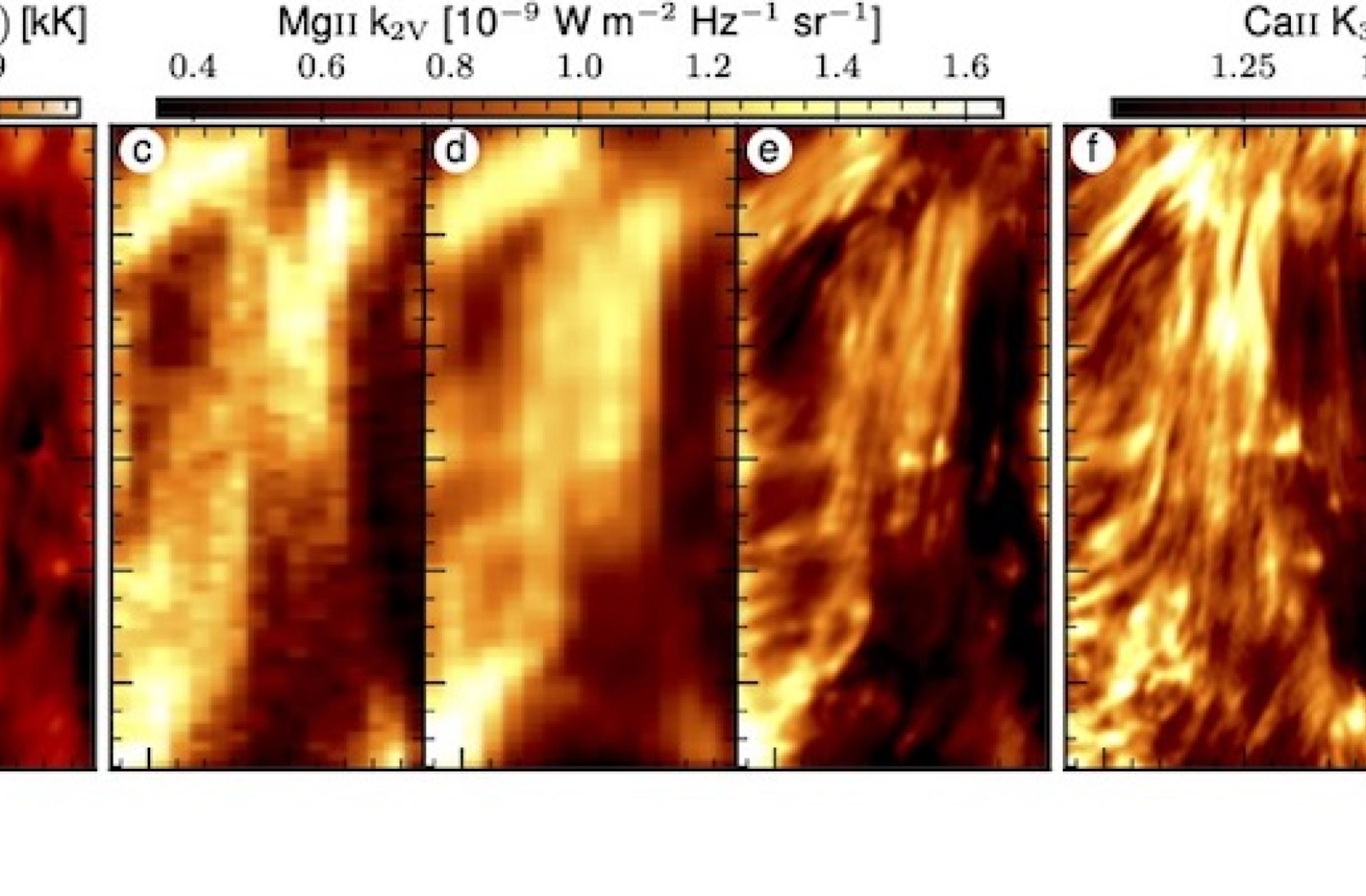
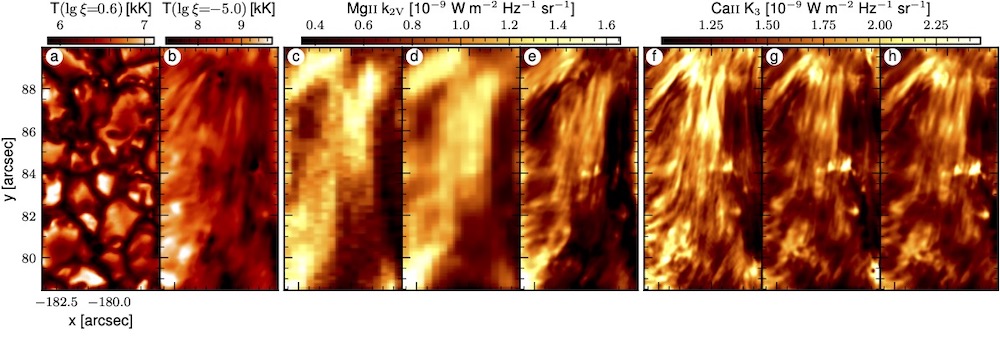
Lidiar con estos sistemas requiere un esfuerzo titánico, tanto a la hora de construirlos como de resolverlos, pero tiene su recompensa como se desprende del panel de la derecha de la Ilustración 2. Para su obtención, hemos realizado una inversión multi-resolución en la que hemos incluido en el proceso de modelado la degradación de cada región espectral, incluyendo la PSF del telescopio de IRIS. La mejora en los modelos ajustados es, a nuestro parecer, impresionante, siendo esta nueva inversión, capaz de recuperar las estructuras de pequeña escala que la inversión tradicional (panel central) es incapaz de resolver. De hecho, una vez que tenemos el modelo final, podemos sintetizar el espectro en todas las ventanas espectrales sin incluir los procesos de degradado. Por tanto, este tipo de reconstrucción en el que incluimos la PSF puede entenderse como una de-convolución de los datos a través de un modelo de atmósfera estelar, dado que el modelo ha sido derivado compensando el efecto de la PSF. La ventaja es que los datos sintéticos no contienen el ruido de la observación (aunque la reconstrucción del modelo sí está afectada por el ruido). La ilustración 4 muestra resultados de una inversión con datos reales de un grupo de datos adquirido con IRIS y con el SST. En este caso, los datos de Mg II k tienen una resolución (panel c) mucho más baja que los del resto de líneas (panel f).

En este contexto es posible que surja la pregunta, ¿por qué queremos obtener modelos de tan alta resolución espacial? La respuesta es que hay muchas aplicaciones en las que se requiere alta resolución espacial. Por ejemplo, para derivar metalicidades o la edad de las estrellas de un cúmulo de estrellas se querrá resolver (separar) la información de cada una de las estrellas. O para estudiar regiones de formación estelar en observaciones de galaxias, podríamos combinar datos obtenidos en la línea de Lyman α y Hα de forma simultánea. En nuestro caso, la principal motivación es el estudio de la disipación o deposición de energía en la cromosfera del Sol. El hecho de tener en cuenta la degradación instrumental permite, por una parte, ajustar los observables sin necesidad de modificarlos (por ejemplo, a través de operaciones de deconvolución o interpolación), y a la vez, encontrar el modelo (la solución) que es compatible simultáneamente con todos los observables.

La fotosfera y la cromosfera solar no están en equilibrio radiativo ya que, si lo estuviesen, la cromosfera estaría mucho más fría de lo que las observaciones sugieren. Éste constituye lo que se conoce como el problema del calentamiento cromosférico. Además, dado que el transporte energético por convección termina en la base de la fotosfera, debe de haber otros procesos físicos que transportan y depositan la energía en la cromosfera (a parte del transporte por radiación que también contribuye, pero no es suficiente). El problema actualmente ha evolucionado, ya que se han propuesto muchos mecanismos que probablemente contribuyen a transportar y depositar energía: difusión ambipolar, disipación Óhmica, transporte por ondas y frentes de choque, reconexión magnética, y muchos más. Así, la pregunta en la actualidad ha evolucionado a ¿en qué medida contribuye cada uno de estos procesos en las diferentes estructuras de la cromosfera? Dado que en todos estos procesos la disipación de energía ocurre a muy pequeña escala, este problema sólo puede estudiarse con observaciones de muy alta resolución espacial.

Por ejemplo, bajo la aproximación magneto-hidrodinámica, podemos escribir algunos de los procesos que disipan energía en términos de un producto de una difusividad por un término proporcional a la corriente eléctrica. Las corrientes eléctricas aparecen en la atmósfera solar cuando el campo magnético cambia mucho en escalas espaciales pequeñas y suele formar cortinas o láminas que normalmente denominamos lámina de corriente eléctrica. Matemáticamente el vector de corriente eléctrica (J) viene dado por J =∇×B/µ₀, donde B es el vector de campo magnético y µ₀ es la permeabilidad magnética en el vacío. Cuando dos parches magnéticos con polaridades opuestas entran en contacto, también se forma una lámina de corriente dado que por definición el gradiente del campo es enorme en la superficie de contacto.

En este sentido, podemos escribir la disipación Óhmica como Q_O=η_OJ², donde η_O es el coeficiente de difusión Ohmica. Igualmente, podemos describir la disipación por colisiones entre átomos neutros con partículas cargadas (difusión ambipolar) como Q_a=η_aJ_⊥², donde η_a es el coeficiente de difusión ambipolar y J_⊥ es la componente perpendicular a la dirección del campo magnético. La Ilustración 5 muestra mapas del coeficiente de difusión ambipolar y Óhmica en la cromosfera de una región activa que contiene bucles cromosféricos (Morosin, R. et. al. en prep.). Aunque en este caso no hemos mostrado información del vector de corriente eléctrica, la distribución presentada en esos mapas sugiere que la difusión ambipolar podría jugar un papel más importante que la difusión Óhmica en este tipo de estructuras. Sin embargo, mientras que las difusividades dependen típicamente de la densidad, densidad electrónica y del grado de ionización del plasma, el vector de corriente eléctrica depende de las derivadas espaciales del campo magnético. Y aquí es donde nuestro método es de vital importancia, ya que optimiza la resolución espacial de los modelos reconstruidos en la inversión.

La principal limitación que tenemos en estos momentos es que todos los códigos de inversión NLTE que existen actualmente operan en una malla vertical de profundidad óptica o de columna de masa. Además, no se impone un equilibrio de presiones horizontal, por lo que no se pueden calcular estas derivadas espaciales del vector de campo magnético para estimar el vector de corriente eléctrica. Muy recientemente, Pastor Yabar et al. (2021) demostraron, usando un código de inversión LTE en la fotosfera, que se puede reemplazar la imposición de equilibrio hidrostático por equilibrio magneto-hidrostático, que además permite de forma natural trabajar en mallas cartesianas y garantiza equilibrio de presiones horizontal (véase la ilustración 6).

Actualmente estamos trabajando en la implementación de una técnica similar en nuestro código de inversión NLTE para poder finalmente empezar a estimar y separar las contribuciones de los diferentes modos de calentamiento cromosférico en el Sol. Este proyecto está financiado por ERC a través de los prestigiosos programas Starting (2017, SUNMAG) y Consolidator (2023, MAGHEAT).

Referencias:

- de la Cruz Rodríguez, J.; A method for global inversion of multi-resolution solar data; 2019; A&A 631, A153
- De Pontieu, B., Title, A. M., et al.; The Interface Region Imaging Spectrograph (IRIS); 2014; SoPh 289, 2733
- Morosin, R., de la Cruz Rodríguez, J., et al.; Reconstruction of the magnetic field vector in chromospheric loops; in prep
- Pastor Yabar, A., Borrero, J. M., et al.; Inference of electric currents in the solar photosphere; 2021; A&A 656, L20
- Scharmer, Goran B., Bjelksjo, Klas, et al.; The 1-meter Swedish solar telescope; 2003; SPIE 4853, 341
- Vissers, G. J. M., de la Cruz Rodríguez, J., et al.; Dissecting bombs and bursts: non-LTE inversions of low-atmosphere reconnection in SST and IRIS observations; 2019; A&A 627, A101

Descargar artículo en PDF